Let k be the number of elements common to all three sets, u be the number of elements in both A and B but not C, and v the number of elements that are only in B.
(Note: The choice of independent variables is arbitrary. From among the seven components we could use the three given conditions to express any three in terms of the other four, and a more “symmetric” choice actually gives a neater version of this proof)
Since u+v is the number of elements in B but not C, the same number must be in both B and C. k are in all three so there must be u+v-k in B and C but not A.
Now let w be the number of elements in C only. Then the total in C but not A is (u+v-k)+w=u+v+w-k, and since there are k in the common set, the number in A and C but not B must be u+v+w-2k.
Since the total number in A must be twice what’s shared with B, that is 2(u+k), the number that are only in A must be (u+k)-(u+v+w-2k)=3k-v-w.
If that is not all clear, then the following diagram might help:
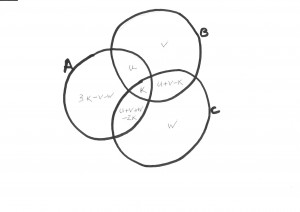
In terms of the independent variables k,u,v, and w, we get
a=2(k+u)
b=2(u+v)
c=2(u+v+w-k)
and our objective is to find extrema of
R=a/c=(u+k)/(u+v+w-k)
for positive integer values of k,u,v,w with u+v-k≥0 , u+v+w-2k≥0, and 3k-v-w≥0.
Equivalently, we could take k=1, look for rational values of u,v,w and rescale at the end to get integer solutions.
So we’re looking at R=(u+1)/(u+v+w-1) with u,v,w≥0, u+v+w≥2, and 3≥u+v≥1
For fixed v and w, R->1 as u->infinity and is monotone in the domain so there are no interior critical points.
We can therefore restrict our attention to the boundary.
On u+v=1, we have u=1-v≤1,
so R=(u+1)/w=(2-v)/w≤2 (since w≥1 since u+v+w≥2);
On u+v=3, R=(4-v)/(2+w)≤2; and finally
On u+v+w=2, u=2-v-w, and so
R=(3-v-h)/(2-1)≤3
So R is never greater than 3, and the bound is attained when v=h=0 (which corresponds to the example cited earlier)
