view as .doc

Module 2

 Functions

2.3

 Operations on Functions

Reading Guide (for Text section 2.7)

 

Algebraic Operations on Functions (see text pp189-190)

 

Q1

The definitions of sums, differences, products, and quotients of functions are all straightforward. Of course the result cannot be defined unless all of its pieces are. So the domain of an algebraic combination must be included in the intersection of those of all its components. But if the combination is a quotient the denominator must not be zero.

As an exercise in set notation, try writing these statements as set equations using  for the domain of f. (see answer #1)

 

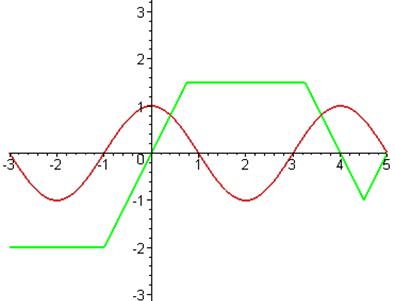
Q2

The graph of a sum or product can be obtained from the graphs of its terms or factors by adding or multiplying ordinates point by point.  After plotting a number of points this way, the graph of the result starts to become clear. Try using these ideas to sketch graphs of f+g and fg  for f and g having the graphs given below. (see answer #2)

 

 

 

 

 

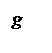
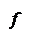
Q3

For the case of a sum of two terms, if one of them is zero the sum is just equal to the other one. So, at the x-intercept of one, the sum graph will be at the same height as the other. Your sum graph should have this property, and you should also note that in an interval where f is constant, the sum graph looks just like part of the g graph shifted vertically. What are the corresponding properties of product graphs? (see answer #3)

 

Composition of Functions (see text pp191-196)

 

The composition operation corresponds to feeding the output of one function as input into the other - much as the output of a radio tuner is fed into an amplifier. We can think of the tuner as a function whose input is the radio signal and whose output is a weak audio frequency signal. If we call the tuner T, and the radio signal r, then  is the weak audio signal produced by the tuner. This is what gets fed into the amplifier. If we call the amplifier , then  represents its output when the input is x. If the amplifier is getting its input from the tuner, then , so the final output is .

The composite function  then corresponds to the connected pair which might be put in a cabinet and sold as a new kind of unit.

 

In order for x to be in the domain of  we need to be able to make sense of , so x must be in the domain of g and  must be in the domain of f.

Thus  

In terms of the radio example, the signal must be suitable for the tuner and the output of the tuner must be

 

In the text’s Example 5 on page 193, given values of f and g are used to determine values of  for various values of x.

 

Q4

The given values could also be provided by means of graphs, as in Exercise 19 on p.151 of the text’s Section 2.4. What are , and  in that case? (see answer #4)

 

 

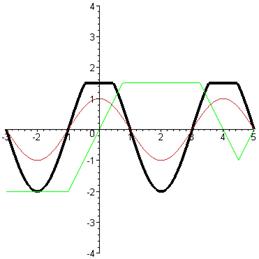
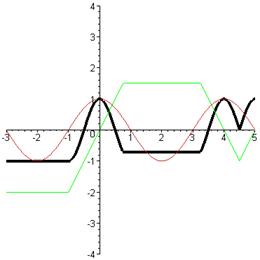
Q5

For the functions f and g graphed in Q2 on the previous page,  the composite functions  and  are graphed below. Can you tell which is which? (see answer #5)

 

(a)                                                                   (b)

    

 

 

Further Practice

 

Check your understanding and practice for speed by working through some of the Exercises on pages 196-199 of the text.

Do enough of the odd numbered questions of each type to convince yourself that you can get the right answers. (Note that, as usual, the answers are in the back of the text and complete worked solutions are in the student study guide - but try to avoid looking at answers or solutions until you have made your own best effort)

 

As a minimum you should do ##3, 13, 23, 37, 41, 43, 47,  51,  and 53.