Module
3 

3.1 

Quadratic Functions
In the shoe store problem it was convenient
to approximate the dependence of sales on price by a linear function.
But what the manager wants us to maximize is the total weekly revenue. And the total amount we take in each week is the amount of each sale times the number of sales.
i.e.
,
or, using R for revenue
You should recognize that this is an example of a quadratic function of p.
(Quadratic functions are function of the form ,
with
.)
Graphing Quadratic Functions
From your reading of Section 2.6 of the text you should have been reminded of how to locate all of the following features of the graph of a quadratic function:
- The y-intercept (value of ) is given by
.
- The x-intercepts
(also known as “roots”) can be found by solving for x in .
Q1
This can be done either by factoring, or by
completing the square, or by using the “quadratic formula”. You should recall
that the number of real roots can be either 0, 1, or 2, depending on the value
of the discriminant. How?(see answer # 1);
- The vertex (which gives the highest or lowest point on the graph) can be found
either by completing the square, or by
using the fact that it occurs at .
Q2
As an application of these ideas, sketch a
graph of the shoe store’s weekly revenue as a function of price. Identify all
of the features mentioned above, and tell the owner what price will maximize
her revenue. (see answer #2).
Determining Quadratic Functions From Their Graphs
Q3
We saw above that a linear function is
determined by two points. For a quadratic, we can do the same with three
points. Try to find the quadratic function whose graph includes the points
(-1,0), (2,0), and (0,1). (see answer #3)
We can manage with just two points if we are told one of them is the vertex. Example #5 in Section 2.6 of the text is a problem of this type.
Further Practice re Quadratic Functions
Check your understanding, and practice for speed, by working through some of the exercises on p183-188 of the text. Do enough of the odd numbered questions of each type to convince yourself that you can get the right answers.
As a minimum, try #3,9,13,19,23,29,33,39,43,51.
Answers to Questions re Quadratic Functions
1. The
discriminant is given by the expression .
If it is positive, then there are two roots
(given by ).
If it is zero, then both of these give the
same result ( ), so there is just one root.
And if it is negative, then the radical is undefined, so there are no real roots.
Note: When the discriminant is zero, the quadratic is actually a perfect square,
,
and since the factor
occurs twice, we often say that
is a “double root” or a root of multiplicity two.
2. From
the equation
we could locate the vertex using
or, just by noting that the axis of
symmetry of the parabola must be midway between the intercepts, which we can
see from the factored form are at
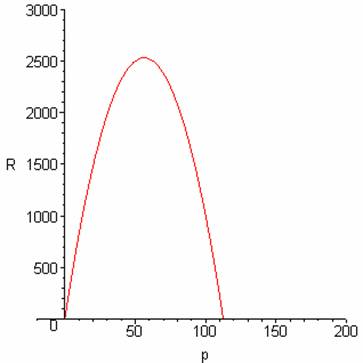
Thus, from the point of view of maximizing revenue, the best price to charge would be $56.25 per pair, and the revenue in this case would be $2531.25 per week.
The graph of can easily be drawn once we have located its
intercepts and vertex:
3. Just as for the corresponding linear problem, there are various ways to do this.
One is to write the given conditions as
three equations in three unknowns, using the facts that , to get
,
and then to solve by elimination or substitution.
First note that the last equation gives .
So
.
Then using the first equation we get ,
and substituting this into the second we get
.
This gives ,
and so
,
and so
.
A quicker method is based on the fact that
two of the given points are x-intercepts.
In fact we could get a graph going through these two points just by taking .
But this function gives which is not the correct
y-intercept. Adding 3 would give the right y-intercept, but by shifting the graph up, it would change the x-intercepts so is NOT a good idea. On the other hand, multiplying by a constant just stretches the graph leaving the x-intercepts fixed.
So we might try ,
and use the y-intercept condition to
find a .
In fact, gives
.
So , which
agrees with the previous answer.