Module 5-I – Review of Triangle Trigonometry
Section 5-I.1 – Geometric Background Review
Introduction
The basic idea on which the whole of trigonometry is based is that triangles (and other objects) can have the same shape but different sizes, and that if the angles of two triangles are equal, then the corresponding sides are in proportion. Such triangles are then said to be similar triangles. Trigonometry starts with right angled triangles, for which the side lengths are related by Pythagoras’ Theorem. This section reviews these ideas, which are fundamental to trigonometry as well as being important in their own right.
Section Learning Outcomes
By the time you have completed this section you should be able to:
· Identify similar triangles in a geometric diagram, and use the similarity to compute unknown lengths in terms of known ones
· Identify right angled triangles in a geometric diagram, and use the pythagoras’ theorem to compute unknown lengths in terms of known ones
· Identify the basic geometry involved in various applied situations and solve problems arising from such situations
Study Plan
1. Read the following Study Notes and Discussion, and make sure that you have absorbed the main points by answering the questions.
2. Follow the instructions regarding Further Practice.
Study Notes and Discussion
As mentioned in the introduction, similar triangles and Pythagoras’ theorem are fundamental to the understanding of trigonometry.
Similar Triangles
Two objects are said to be similar if they have the same shape but possibly not the same size (like near and far views of the same object). For triangles, we can think of the “shape” as being determined either by the angles or by the relative lengths of the sides. In fact, these approaches are equivalent. It is a theorem of geometry that if two triangles have the same angles then the ratios of corresponding sides are equal. Triangles with this property are said to be similar triangles. In the picture below, a copy of the small triangle has been fitted into each corner of the big one so we can see that the angles are equal.
![]()
![]()

The statement that ratios of corresponding sides are equal can be interpreted in two equivalent ways, both of which are useful. For example, in the above picture we can compare corresponding sides between triangles to say that or compare ratios of corresponding pairs of sides within each triangle to get . But of course, by cross-multiplying we see that these are equivalent.
Note: Because similarity involves matching corresponding sides, when we describe two triangles as similar it is important to indicate their vertices in matching order. So for example, where above we have , it would not be correct to write .
A simple application of similarity would be to determine the length x in the picture below.
(The matched sets of arrowheads denote that the lines are parallel.)
 What is x?(see answer #1)
What is x?(see answer #1)
This next one is a bit
trickier. (The
symbol ![]() denotes a right
angle.)
denotes a right
angle.)
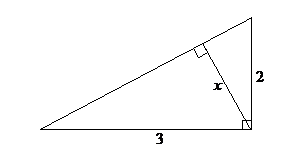 What is x?
(see answer #2)
What is x?
(see answer #2)
Pythagoras’ Theorem
The fact that in a right triangle “the square on the hypotenuse is the sum of the squares on the other two sides”, and conversley that if the sides of a triangle are related this way then the angle opposite the longest side is a right angle, is perhaps the most famous theorem in all of mathematics. Of course it is already familiar to you, but we mention it again here to remind you that it is something you should always keep in mind when looking at situations involving right angles (like the second of the two examples above).
Applications
Here is a simple applied problem using similarity:
A surveyor whose eye level is 1.5m. above the ground sights the top of a tree at a distance of 100m. in line with the top of a 2m. pole held vertically by an assistant 5m. away. How high is the tree?(see answer #3)
This one combines similarity with use of Pythagoras’ theorem:
A 4m ladder leaning against a 2m fence is initially vertical (right up against the fence), and its lower end is being pulled steadily away from the fence. If a leaky bucket of paint hanging at the top of the ladder is dripping steadily, how far behind the fence are the dripmarks falling when the base of the ladder is 2m from the fence? (see answer #4)
Tip:If you have difficulty visualizing the situation try building a model, with something like your caculator as the fence and a ruler or folded page as the ladder.
In the Further Practice for this section we will identify a number of problems from the early parts of the text where the use of similar triangles and/or Pythagoras’ theorem are involved.
Further Practice
Similar triangles and Pythagoras’ theorem are relevant in a number of the problems in Chapters 1 and 2 of the text. For example Section 1.4 #71,79,87; Section 2.4#73,75,76; Section2.7#50; and Section 2.Rev#79,80,81.
It would be a good idea to work a few of these, say at least
Section 1.4#79; Sec2,Rev#79,81.