Module 5-II – Trigonometric Functions
Section 5-II.1 – Definitions and Evaluation
Introduction
If, for each value of t between 0 and 90, we construct an angle of , build a right triangle, and measure its sine ratio, then the result will define a function of t with . If we use a different method of measuring angles then for a given value of the number t we’ll be looking at a different angle and so get a different result. So we’ll get a different function. For example, the functions , and are both different from .( If you put in a particular number, like 1/4, for t , they will give different results). Of course, since an angle of t degrees is the same as an angle of radians, we have and so the functions are related, but they are not the same.
It turns out that the functions defined using radian measure are more convenient for many purposes (especially in calculus) so these are the ones we’ll focus on, and it is just for these that we use the name of the trigonometric ratio as the name of our function. (So, we’ll use the name just for the case of above.) This section is devoted to introducing these functions and studying their basic properties.
Section Learning Outcomes
By the time you have completed this section you should be able to:
· State the “unit circle” definitions of the trigonometric functions
· Use the definitions to evaluate these functions (exactly if possible)
Study Plan
1. Read the following Study Notes and Discussion, and make sure that you have absorbed the main points by answering the questions.
2. Read sections 5.3 and 5.4 of the text
3.
Follow the instructions
regarding Further Practice.
Study Notes and Discussion
Need for Units
As pointed out in the introduction to this section, if we want to use the trigonometric ratios to define functions of a real number variable, then it is necessary to decide what system of units is to be used to relate angles and numbers. Because of the way it relates angles and distances, the radian measure of angles turns out to be more convenient for many applications (especially in Calculus), so, in Section 5.3 of the text, the trigonometric functions of a real variable, t, are defined as the corresponding trig. ratios for an angle of t radians.
i.e. , etc.
Circle Picture
Another way of stating the above definition is to say that cos(t) and sin(t) are the x and y coordinates of a point on the unit circle at a distance of t units from the positive x axis as measured counterclockwise around the circumference of the circle.Why? (see answer #1) The other trig functions are then defined in terms of sin and cos by the same relationships as for the corresponding ratios.
 This “unit
circle definition” has the advantage that it doesn’t just work for
acute
angles. In fact it makes sense for arbitrary real values of t.
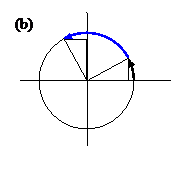
For example, to find cos(10) we can
go 10 units around the circle. (see below)
This “unit
circle definition” has the advantage that it doesn’t just work for
acute
angles. In fact it makes sense for arbitrary real values of t.
For example, to find cos(10) we can
go 10 units around the circle. (see below)
Since the circumference is , going 10 units around takes us more than one full revolution, but that’s ok. Another half revolution takes about 3.14 more units and we come to the end of our 10 unit trip just a bit further on as shown in the picture.
The x-coordinate of the endpoint is by definition cos(10), and by measuring on the graph we see that it’s about
-0.85 . Using your calculator (in radian mode) you should be able to check that this is about right.
If you estimate the y-coordinate of the terminal point in the above picture you should get about -0.55, and if you check on your calculator you should see that this is a pretty good estimate for sin(10).
For negative values of t , we follow the same convention as for negative numbers on the number line – that is we go in the opposite direction. So to find cos(-10) we go 10 units clockwise. So making a picture like the one above for we find cos(-10)=cos(10) and .
Try using the circle picture to evaluate each of the following as accurately as you can :-
a) b) c) d) cos(1) e) sin(30) (see answer #2)
Note that with this unit circle approach there is no need to memorize a set of rules for the signs of the trig functions. They are just the signs of the corresponding coordinates of the point on the unit circle. So the table and mnemonic on page 384 of the text can safely be ignored. (This doesn’t mean that you don’t need to know what they say, just that once you understand the circle picture these facts will be obvious.)
The Basic Graphs
The graph of can be drawn by just tracing the height of the point as it moves around the unit circle with t being the arc length from the x-axis (counterclockwise). If you imagine moving around the circle in the picture below, then, as it does so, the graph on the right will be traced out. Many important phenomena have similar infinitely repeated regular oscillations and this is why trigonometric functions are so useful even outside of geometry.

Note: We would get a similar picture if we used different angular units rather than radians except for the fact that the horizontal distance on the t-axis would no longer exactly match the arc length but rather would be some multiple of it. So the graph would be stretched out unless the t-axis is re-scaled. What distinguishes the case of radian measure is the equality of arc length and distance along the t-axis. If a point is moving counter-clockwise around the circle, then as it passes it is moving directly upwards, and so, for small , the y-coordinate is almost exactly equal to the arc length. I.e. for small . This means that the graph of is very closely matched near the origin by the diagonal line ,(at to both axes if the scales are equal).
Some Basic Identities
The unit circle picture also allows us to easily establish various identities concerning the trig functions.
For example, the equation of the circle ( ) gives us the 'pythagorean identity',
.
Other identities express relationships between trig ratios of different angles:
(i) one such is the 'negative angle relations' and which are illustrated in Figure 12 on page 396 of the text;
(ii) another is the 'periodicity relation'
which corresponds to the fact that going a distance around the unit circle brings us all the way back to where we started;
(iii) and another is the pair .
These three are all illustrated below (which is which?)(see answer #3)

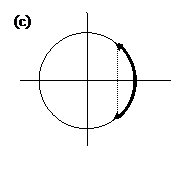
Exercise:
Use similar pictures to show that (answer #4)
and to derive formulas for and .( see answer #5)
Basic Trigonometric Equations
We can also use the unit circle picture to go the “other way” and determine t from the value of sin(t) or cos(t). This amounts to solving for t in equations of the form , and . Because they are expressed in terms of trig functions, these are called trigonometric equations.
For example, to solve we need to find the numbers t for which the point has y-coordinate equal to c. These would be the t-values for intersection points of the circle with the horizontal line . For , the points are shown in the picture below.
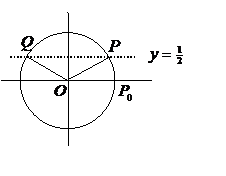
We know that .
How? (see answer #6)
So and is one solution.
By symmetry we see that , so is another solution.
And adding any multiple of brings us back to the same point so we find that the general solution is , where n can be any whole number.
Even when we can’t determine an exact value, we can use the circle picture to estimate the solutions. A bigger picture is easier to measure on, and it helps to have the arc lengths labelled as in the text’s illustration for Exercises 69-72 on page 406. Try using that one to estimate the solutions of . (see answer # 7)
Note that the calculator’s button can be used for such problems to get a better approximation. It only gives one of the possible solutions, but the others can be found by reflecting across the y-axis and adding multiples of .
Similarly, to solve we look for intersections with the vertical line . Again there are two points of intersection, but this time placed symmetrically across the x-axis, and each corresponds to an infinite family of t values by adding multiples of .
For the case of , it is neither x,nor y that we must match but rather their ratio , which is just the slope of the ray from the origin to the required point. So to solve , for example, we just draw the line , and check where it crosses the circle. By eye we can read off that one point is at (calculator gives 1.107..), and the other one is exactly halfway around the circle - which we can reach by adding .
Further
In section 5.4, the text uses some of the basic identities discussed above (and in the text’s section 5.3) to express the trig ratios for any angle in terms of a “reference angle” between and (i.e. between 0 and ).
You may find that by trying to explain it in words the book makes the “reference angle” approach seem more complicated than it really is. For example on page 409, the pictures in Figure 2 may be easier to understand if you don’t read the text beside them. In fact you can evaluate trig ratios for general angles just as easily by using the unit circle, measuring off the angle (equal in radians to the distance around the circumference) and using basic trigonometry on the right triangles joining the terminal point to the coordinate axes to determine the x and y coordinates (of the point corresponding to the given angle.)
Try using this approach to solve the text’s Example 2 on page 410. (see answer #8)
The text material about finding angles from trig ratios on pages 411-414 can also be understood most easily in terms of the unit circle picture as we have described above.
Try using the circle approach to solve the text’s Example3 on page 413. (see answer #9)
Further Practice
Try enough of the odd numbered questions in the text sections 5.3 and 5.4, using the solutions guide if you need to, until you feel able to do similar questions on your own.
From section 5.3 you should do at least #3,13,23,33,53,69, and 73, and from section 5.4 at least #7,27, and 39.