Mock Final Exam
This practice exam is intended to give you an idea of the length and difficulty of the actual final exam. The questions on that exam will not necessarily be of exactly the same types as these, but will be similarly distributed over the course and with a similar level of difficulty.
You will be allowed two hours to complete the actual exam, so if it takes you longer to do this one, then you should keep practicing until you can get through something similar in two hours.
Marks (Total 100)
On the actual exam, you will be allowed to
use a scientific or graphing calculator, but no communication devices, or notes
(including electronic files). Except when asked for an approximation, you
should give exact answers where possible. For full marks, all appropriate work
must be shown and your work will be judged for clarity of explanation as well
as for correctness of results.
---------------------------
1.
[5]
For ,
compute and simplify to show that it is proportional
to
2. For each of the cases described below, give an equation (of the form ) for the graph that results
[4]
a) when the graph of is shifted left 4 units then reflected across the x-axis, and finally
shifted down 2 units;
[4]
b) when the graph of is reflected across the y-axis and then shifted 4 units to the right;
[4]
c) when the graph of is shifted 4 units to the right and then reflected across the y-axis.
3. a) Sketch a graph of a function f that has all of the following properties:
[5]
(i) f has x-intercepts at 0,
-2, and -4.
(ii) is an asymptote for f
(iii) f is decreasing on , and increasing on
(iv) as
(v) for
[5]
b) Find a possible formula for a rational function f with these properties.
4. A computer-generated graph of the function
is shown here:
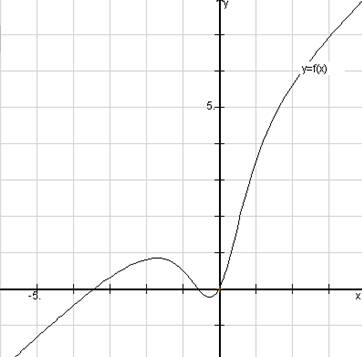
[6]
a) Determine exact expressions for all of the
intercepts, asymptotes, and holes in this graph (including any that are not
apparent in the above picture).
[2]
b) What is the domain of the function ?
[2]
c) Sketch the graph of for
5.
[5]
An air plane flying due East at a steady rate
of 300 km/h passed over a mountain top at
[5]
(a)
Determine D, the distance between the
two planes as a function of t, the
number of minutes after
(b) Air safety regulations for the area forbid any two aircraft to come within one kilometer of one another. Was there a violation in this instance?
6.
[8]
According to “
7. The perceived loudness, L , of a sound is proportional to the logarithm of its physical intensity, I. For loudness measured in decibels (dB), the difference in loudness of two sounds is given by the formula where and are the intensities.
[2]
a)If the second sound’s intensity ( ) is 100 times the first, how much louder is
the second sound in decibels?
[3]
b) By what factor must the intensity of sound
be increased in order to increase its loudness by 5dB?
[3]
c) If the intensity of a sound falls off in proportion to the inverse square
of the distance from the source, by how many decibels will the perceived loudness be reduced by doubling one’s
distance from the source?
![]() 8. A railway company is
building a new railroad. Surveyors wish to measure the height of a hill and the
length of a tunnel to be cut through the base of the hill. At the East end of the tunnel, the surveyors
measure the angle of elevation of the top of the hill to be .
When they move 80 metres further East, the angle of elevation to the top of te
hill is .
From a point 120 metres to the West of the West end of the tunnel, the angle of
elevation of the top of the hill is .
8. A railway company is
building a new railroad. Surveyors wish to measure the height of a hill and the
length of a tunnel to be cut through the base of the hill. At the East end of the tunnel, the surveyors
measure the angle of elevation of the top of the hill to be .
When they move 80 metres further East, the angle of elevation to the top of te
hill is .
From a point 120 metres to the West of the West end of the tunnel, the angle of
elevation of the top of the hill is .
![]() (a) Find the height of the hill, h.
(a) Find the height of the hill, h.
(b) Find the length of the tunnel, l.
9. At 6am, the temperature was and rising, and is predicted to vary according to the formula , with a period of 24 hours, a low of , and a high of .
[4]
a) Sketch a rough graph showing the
dependence of on t.
[2]
b) Use your graph from part (a) to estimate the time of day at which the high will occur.
[2]
c) Use the graph to estimate for how many hours of the day the temperature exceeds .
10. Find exact expressions for all real solutions for each of the following:
[4]
a) 2 + log2x = 2 log2(x+1)
[4]
b) sec(x) - cos(x) = 2
[4]
c) 1 - 2 sin(2x) > 0
11. For each of the following equations, EITHER prove that it is an identity, OR find a value for x at which it is not true:
[3]
a) tan(x) + cot(x) = sec(x) csc(x)
[3]
b) ln(cos2x + 2sin2x) = 0
[3]
c) arcsin(sin x) = x