Mock Final - Solutions

Mock Final Exam

Solutions and Remarks

After you have given it your best effort, compare your solutions with these. The comments following each solution are partly to provide some additional explanation, partly to point out some common mistakes, and partly to suggest where you can look to review the topic and find additional practice problems of a similar type.

1. For , compute and simplify to show that it is proportional to

Solution:

Comments:

The ability to correctly read function notation in an expression like this is vital for calculus. If, on the exam, you misread as then you will get no part marks for the question (and are probably not ready to go on to calculus).

For more examples of this type, see Example #5 and Exercises ##5-14 and ##41-44 in Section 2.1 of the text, and also Example #4 and Exercises#51 and #52 in Section 6.3.

If you got this one wrong, then you should do all of those before writing the final.

2. For each of the cases described below, give an equation (of the form ) for the graph that results

a) when the graph of is shifted left 4 units then reflected across the x-axis, and finally

shifted down 2 units;

Solution:

Comments: First replace the x with x + 4 (remember “reach right to pull left” from Unit2.2)

then multiply the result by -1 (reflecting across the x-axis)

and finally subtract 2 (to shift the graph down).

b) when the graph of is reflected across the y-axis and then shifted 4 units to the right;

Solution:

(which is the same as )

Comments: First multiply x by -1 (to reflect across the y-axis)

then replace the x with x - 4 (remember “reach left to pull right”)

c) when the graph of is shifted 4 units to the right and then reflected across the y-axis.

Solution:

Comments: First replace the x with x – 4, then multiply x by -1

Note that the order matters!

The question doesn’t specify the function f so you must write your answer in terms of a general f.

If you plug in a particular function you will not get the marks.

Exercises ##41-44 in Section 2.1 of the text ask you to produce similar formulas, and ##31-38 in the same set go the other way (asking you to give a verbal description of the transformation).

3. a) Sketch a graph of a function f that has all of the following properties:

(i) f has x-intercepts at 0, -2, and -4.

(ii) is an asymptote for f

(iii) f is decreasing on , and increasing on

(iv) as

(v) for

Solution:

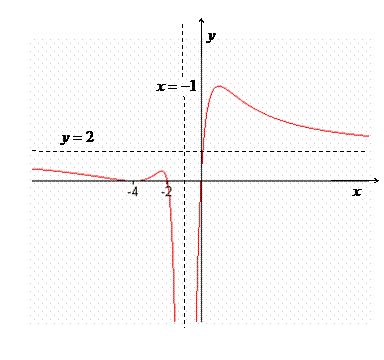
b) Find a possible formula for a rational function f with these properties.

Solution:

Comments:

For practice in drawing graphs satisfying specified conditions see the text’s Section 2.1 Exercises #29 and #30, and to review the use of such information to determine formulas see Unit 3 (especially Q2 in Unit3.3 and Q6 in Unit3.4) and for more practice with these ideas, look in the text at Example 3 in Section 3.2, Example 1 in Section 3.3 and exercises ##7-14and ##41-44 in Section 3.3, ##41-44 in Section 3.5. (For the special case of quadratics you might also look at ##23-32 in Section 2.3.)

4. A computer-generated graph of the function is shown here.

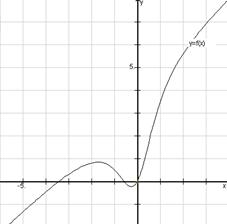
a) Determine exact expressions for all of the intercepts, asymptotes, and holes in this graph (including any that are not apparent in the above picture).

Solution: Since the degree of the numerator is one more than that of the denominator there will be a slant asymptote. Using long division, we get

So , and the slant asymptote is given by

Factoring gives

so the graph agrees with except for a hole x = 0.

Since is undefined at x = 0, there is no y-intercept.

For the denominator is never zero so there are no vertical asymptotes, and the numerator is zero at x = 0, and at

So the hole is at the origin, and the x-intercepts are at

Finally, since the asymptote goes up on the right, so does the graph, and since the net multiplicity at each intercept and at x = 0 are all odd, there are sign changes at each of these points (consistent with the given picture).

Comments:

The approximate values of -0.6 and -3.4 are consistent with the given picture, but it is the exact values which must be given in order to get full marks. The hole is not visible on the computer generated graph, but although the graph appears to go through the origin it is wrong to state that zero is an intercept.

If you had any difficulty with this, review Unit 3.4 (and the text Section 3.5)

b) What is the domain of the function ?

Solution:

In order for to be defined, what is inside the square root must be non-negative.

So we must have . (This is just where the given f graph is above the x-axis.)

Comments:

You would get some part marks for saying that we must have , but it is wrong to say just . Since the question did not specify interval notation, it would be ok to express the solution in terms of inequalities by saying:

“ The domain of g is the set of x-values satisfying either or .”

Note that, since is defined, we include the endpoints at ,

but since is undefined we do not include x = 0.

For more questions on domains involving radicals see the text’s Section2.4 Exercises##21-28

c) Sketch the graph of for

Solution:

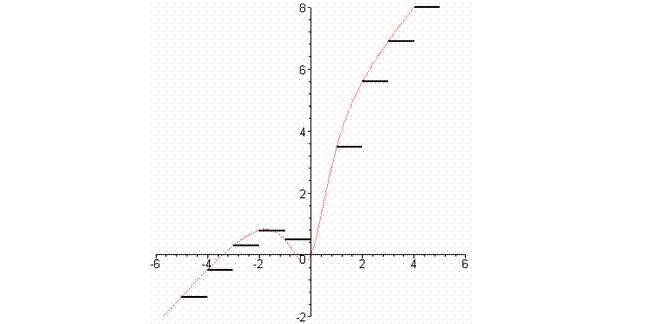
Comments:

The notation was introduced in the text in Section 2.2 (see p162 and Exercises#51&52).

is equal to the value of f at the closest integer to the left of x.

(Note that the result for would be different. In this case the rounding would be applied to the y values after computing , so the result would be to move points down from the f graph to the nearest integer below, and the steps would be equally spaced in height with varying widths.)

5. An air plane flying due East at a steady rate of 300 km/h passed over a mountain top at noon on a summer’s day. Twelve seconds later, another plane, headed North-East at 600 km/h passed by at the same altitude.

(a) Determine D, the distance between the two planes as a function of t, the number of minutes after noon.

Solution:

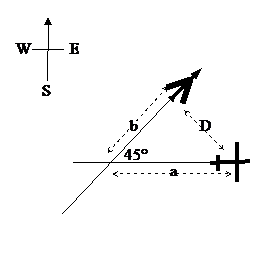
By the Law of Cosines,

Since the first plane is traveling at 300km/h=5km/min,

at t minutes after noon it has traveled 5t km past the mountain. So km

The second plane is traveling at 10km/min, but passed the mountain 12sec after noon so by t minutes after noon it has only been NW of the mountain for minutes.

So km.

So km

(b) Air safety regulations for the area forbid any two aircraft to come within one kilometer of one another. Was there a violation in this instance?

Solution:

The problem here is to see if the distance D was ever less than 1 km. So check the minimum distance.

The minimum value of D occurs at the same time as the minimum value of , and is quadratic.

In fact is minimized at . So the planes were closest to one another at about 15 sec after noon, and the smallest distance (in km) was about So, yes, there was a violation.

Comments: For other questions like part (a) se text exercises like #14 and #15 in Section 7.2, and for another minimum distance problem look at exercise #53 in the text’s Chapter 2 review.

6. According to “Newton’s Law of Cooling”, the temperature of an inert body approaches exponentially toward that of its surroundings. In other words, if T(t) is the temperature of the body at time t, and is the temperature of the surroundings, then the difference decays exponentially to zero, i.e. for suitable constants A and k. This fact is often used in police work, for example to find a time of death. If a detective finds a dead person at a temperature of in a room where the air temperature is , and if the body cools down to over the next hour, then how much earlier was the victim last alive (and presumably at a normal body temperature of so that )?

Solution:

Here the air temperature is the temperature of the surroundings, so ,

and if we measure time in hours after death, then we have (since ). So .

Let be the number of hours until the body was discovered.

We have and .

Thus

and .

and

This gives ,

and since , we get .

So .

So the victim had died about 2 hours and 40 minutes before the body was discovered.

Comments:

This one is tricky because we have two unknowns (the decay rate and the time). But by carefully expressing all of the given information we can find a way to solve the problem. One way to get messed up in problems of any type is to use the same variable name for different values. Note that here we avoided that - by giving a particular name to the time of discovery, and then expressing the later time in terms of it.

7. The perceived loudness, L , of a sound is proportional to the logarithm of its physical intensity, I. For loudness measured in decibels (dB), the difference in loudness of two sounds is given by the formula where and are the intensities.

a)If the second sound’s intensity ( ) is 100 times the first, how much louder is the second sound in decibels?

Solution: Here is 100 times , so

So the loudness difference is 20dB. (i.e. the second sound is 20dB louder.)

b) By what factor must the intensity of sound be increased in order to increase its loudness by 5dB?

Solution:

To get , we need . So which means

So we need , i.e. the intensity must be increased by a factor of (or approximately 3.2)

c) If the intensity of a sound falls off in proportion to the inverse square of the distance from the source, by how many decibels will the perceived loudness be reduced by doubling one’s distance from the source?

Solution:

Here I is proportional to or in other words where d is the distance (and k is the constant of proportionality). If we double the distance, we divide the intensity by four, so

(Alternatively, )

This gives .

So the loudness will be reduced by about 6 decibels.

Comments: The decibel measure of loudness is just one of several applications of logarithms introduced in the text’s Exercises for Sections 4.3, 4.4, and 4.5, and in the Chapter 4 Review Exercises. But you don’t need to learn all of the application subjects. The idea is to be able to recognize and apply the math in a variety of contexts. In whatever applied problem appears on the exam, you will be given any necessary formulas from the area of application. (Not the math ones though!)

8. A railway company is building a new railroad. Surveyors wish to measure the height of a hill and the length of a tunnel to be cut through the base of the hill. At the East end of the tunnel, the surveyors measure the angle of elevation of the top of the hill to be . When they move 80 metres further East, the angle of elevation to the top of the hill is . From a point 120 metres to the West of the West end of the tunnel, the angle of elevation of the top of the hill is .

(a) Find the height of the hill, h.

(b) Find the length of the tunnel, l.

Solution: With all lengths in metres, the situation looks like this:

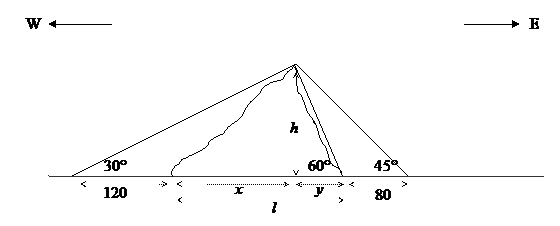
(a)

, so , and so or

So , which gives so

So the height of the mountain is about 189 metres

(b) with and

So the length of the tunnel is about 317 metres.

Comments:

Careful reading helps.

Many students mislabel the distances in a problem like this, so think carefully.

For more practice try any of the text exercises in sections 5.7, 7.1 and 7.2

9. At 6am, the temperature was and rising, and is predicted to vary according to the formula , with a period of 24 hours, a low of , and a high of .

a) Sketch a rough graph showing the dependence of on t.

Solution:

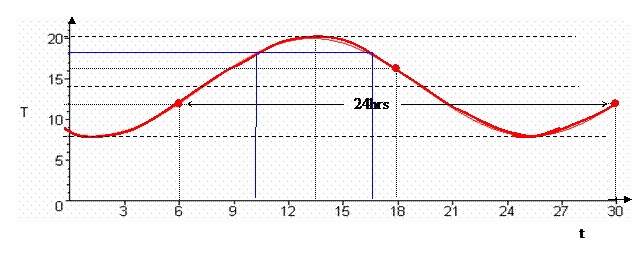
Comments: It helps to first plot the given point at (6,12), then use the 24 hour period to get also (30,12) The fact that adding half a period reverses the sign of the sine term then gives T=14+2=16 at t =18.

Drawing a smooth sine curve through these points and between T = 8 and T =20 then produces the above graph.

b) Use the graph from part (a) to estimate the time of day at which the high will occur?

Solution:

From the graph it looks like about halfway between 12 and 15 at (i.e. about 1:30pm)

c) Use the graph to estimate for how many hours of the day the temperature exceeds .

Solution:

From the graph it looks like from about t = 10.25 to about 16.75 (i.e. about 6.5 hours)

Comments:

In many applications a rough estimate like this is all that is needed, and even when a more accurate answer is needed the rough estimate provides a good check. So there will always be some partial credit given for an answer like the above even when the question asks for more.

If the problem had not specified “to estimate” we would actually need to find exact values for A, B, c, and d, and then solve for t-values giving T=18. This can be done as follows:

The average value of T is , so ; and the amplitude, B , is the variation above and below this, so . Since the period (time for one full cycle) is 24, we must have , so . So . Since , we get .

So .

This is true for and for

But the case with gives T decreasing rather than increasing at t = 6,

(the point on the unit circle moves down as the angle increases). So we can rule out the second case, and since adding has no effect on the result, we can just take which gives

Now we can find the exact answers for questions (b) and (c).

b) For the maximum of T, the sine must be +1. So .

This gives , so .

So our estimate of 1:30pm was pretty close.

c) For T = 18, we need , so

Thus

The different n correspond to different days; to get the two times within the first 24 hours we take n = 0.

And to answer the question we just take the difference

This is about 6.4 so our rough estimate of 6.5 was pretty good!

Note that this kind of analysis might be required on the exam. (Perhaps some of the other questions might be easier in that case though!) Review the questions in Unit 6.2 and the text Section 5.5 (especially the applied ones ##46-62) for the basic graphical ideas, and see Unit 6.4 and the text’s Section 6.6 for more on the use of inverse trig functions for equations which cannot be solved by using special angles.

10. Find exact expressions for all real solutions for each of the following:

a) 2 + log₂x = 2 log₂(x+1)

Solution:

Taking powers with base 2 gives .

So , and so

Thus . So is the only solution.

Comments:

But this won’t earn full marks! After solving by combining logs it is always necessary to check for spurious solutions. In this case the solution does check ok but you must record that you did check. (At x=1, LHS = and RHS = . So they do agree)

b) sec(x) - cos(x) = 2

Solution:

Multiplying through by gives 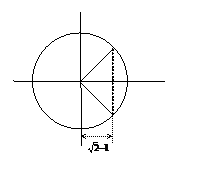, so .

By the quadratic formula,

But is ruled out as a possible value for .

So . Thus .

Comments: Don’t forget that if x is not restricted

then there are infinitely many solutions.

The fact that x can be plus or minus the arccos can be seen

either from the symmetry (evenness) of the cos graph

or from the unit circle picture on the right.

c) 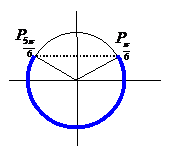1 - 2 sin(2x) > 0

Solution:

This is equivalent to

For , we get , and for the inequality we need the parts of the circle below these points.

For this means ,

and the general solution is where n is any integer.

Thus, for the given problem . So

Comments: The solution of is quite easy to read off from the circle picture above.

11. For each of the following equations, EITHER prove that it is an identity, OR find a value for x at which it is not true:

a) tan(x) + cot(x) = sec(x) csc(x)

Solution: Yes this is an identity.

Comments: The safest way to prove an identity is to transform one side into the other by a sequence of simpler identities as above. Remember the “two-column proof” that -1=1 (squaring both sides gives the same result), and be warned that you will not get any credit for a “proof” which starts with the statement that you are trying to prove.

b) ln(cos2x + 2sin²x) = 0

Solution: Yes this is an identity.

c) arcsin(sin x) = x

Solution: No, this is not an identity.

For example so, at , the two sides are not equal.

Comments:

We discussed and graphed this function at the end of Unit 6.

If you just test with your calculator, you will often get the same result for both sides. In fact,

for , but to be an identity it must be true for ALL x , i.e. the two sides must either both exist and be equal or both not exist. If there is ANY x for which the two sides exist and are different, or for which one side is defined and the other is not, then the statement is not an identity.

(So for example is not an identity unless we add the restriction on the right)