Module 2 

2.2 

(Use this reading guide along with section 2.5 of the text)
Symmetry
(see text pages 156-157)
A function with the property that has a graph which is symmetrical about the y-axis, so once we have graphed one half
the other half comes “for free”. Expressions like
which are expressed in terms of just even
powers of x have this property, so all
such functions are called EVEN functions. Similarly, functions satisfying
are called ODD functions since they include
sums of odd powers.
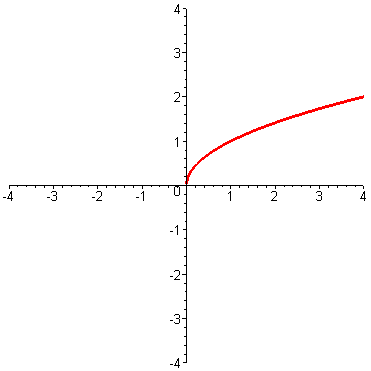
Q1
If f
is either an even function or an odd function then just one half of its graph
is enough to get the rest. Can you draw the complete graph of an even function
and an odd function whose graphs include the part sketched below? (see answer #1)
Shifting
(see text pages 158 and 159)
Adding a positive constant to the value of
a function produces a new function whose graph is moved up
in the direction of increasing y. But adding a positive constant to the
argument x moves the graph to the
left
in the direction of decreasing x.
One way to understand this is to note that
to graph what we plot at
is the y-value
of
.
That is, to find the y-value on our
new graph we look on the old graph at the point c units to the right (if c>0).
But if we reach to the right to find our values but that means that we will
pull them to the left. Thinking “Reach
right to pull left” may help you to remember the resulting effect on the
graph. The apparent difference between x
and y disappears if we note that
is the same as
.
So adding c to the formula for y is the same as replacing y in the equation not by y+c but rather by y-c.
Scaling
(see text pages 160-162)
Q2
The scaling story is
similar.
The graph of comes from
by multiplying all y-values by c
which stretches the graph vertically if
,
and compresses it if
,
(and flips it across the x-axis if c<0).
But for multiplication of x to give the effect is reversed , i.e. if
the graph of squashed sideways rather than
stretched. Can you see how to explain this along the same lines as above for
shifting? (see answer #2)
Combined Operations
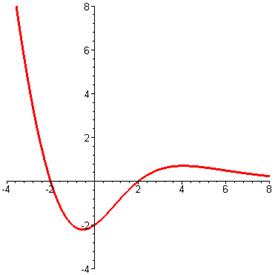
Q3
For situations
involving both addition and multiplication, it is safest to work in stages.
For example, to
graph we need to consider both a shift and a
scaling, but
it may be hard to guess the sequence of operations which produces the desired outcome.
See if you can do it for the function f graphed below. (see answer #3)
![]()
Piecewise Defined Functions
(text pages 162Example8-168)
These come up in applications like tax schedules as discussed on page 165-166.
The absolute value is also an example since
We discussed them also a bit in the previous unit. Can you write the piecewise defined function whose graph is given in Exercise #20 on page 151 from Section 1.4 of the text?
(see answer #4)
The
“greatest integer function” discussed on pp166-167 is important in computing
since it gives the result of “rounding down”. In many computer programming
languages it is called the “floor” function. So .
This is useful for describing anything that goes up in steps like the cost of mailing a parcel as a function of its weight for example, so it is sometimes also called the “postage function”.
Application to Quadratic Functions
In section 2.6 of the text the above ideas
are applied to the special case of quadratic functions i.e. functions of the form
.
The main idea is that by factoring out the leading coefficient, a, and “completing the square” such
functions can be written in a form (
) whose graph is obtained from
just by shifting and scaling.
You might read section 2.6 now, but we will address it again in the next module so it won’t be included in the assignment for this module and you can leave it until later if you prefer.
Further Practice
Check your understanding and practice for speed by working through some of the Exercises on pages 169-172 of the text. Do enough of the odd numbered questions of each type to convince yourself that you can get the right answers.
As a bare minimum you should do ##1,5,17,27,31,37,41,47,51,55 and 65.
You might also experiment with our shift and scale applet to help build your understanding of how these transformations work.