Month: October 2024

Definite values and Eigenstates

A Quoran asks: Once we decide that physical states are represented as vectors in a Hilbert Space and observables as operators, can we deduce that states of definite values of an observable should be eigenstates of the corresponding operator?
 
Not in any conventional sense of the word “deduce”. (It is possible to “represent” physical states as vectors and observables as operators in all kinds of ways that have nothing to do with the representation that is useful in quantum theories.)
 
But if you are talking about the usual connection in quantum mechanics that we make between states and vectors and between observables and (self-adjoint) operators, then that includes also the condition that for the observable represented by operator [math]A[/math], the distribution of observed values, when it is measured in the state represented by vector [math]\psi[/math], is such that the probability of a measurement of [math]A[/math] being in any specified interval [math]L[/math] is given in terms of the spectral projector [math]E_{L}(A)[/math] by the inner product [math]\frac{\langle \psi |E_{L}(A) \psi\rangle}{\langle \psi |\psi\rangle}[/math] (or just [math]\langle \psi |E_{L}(A) \psi\rangle[/math] if [math]\psi[/math] is normalized with [math]\langle \psi |\psi\rangle=1[/math]).
 
And if you are requiring that we decide to adopt that representation, then it does follow (essentially immediately from that extra assumption) that a state in which the observable has a definite value is represented by an eigenvector of the corresponding operator.
 
PS The spectral projectors [math]E_{L}(A)[/math] of any observable [math]A[/math] also correspond to question-type observables giving the value 1 when [math]A[/math] is observed to give a value in [math]L[/math] and 0 otherwise, and the expectation value of any question is just the probability of its value being 1 (ie of the answer being “true”). So the assumption made above actually follows from the simpler version which just says that the expectation values of observables are always given by inner products of the form [math]\langle \psi |A \psi\rangle[/math] where [math]\psi[/math] is a corresponding normalized vector and [math]A[/math] is the corresponding observable (which includes the case of spectral questions about other observables).

Source: (1003) Alan Cooper’s answer to Once we decide that physical states are represented as vectors in a Hilbert Space and observables as operators, can we deduce that states of definite values of an observable should be eigenstates of the corresponding operator? – Quora

A Question About Geometrical Optics

How do you draw the image of the light source through the converging lens if the light sources are located higher than the top of the lens (it is not allowed to extend the lens)?

In a conventional diagram of the geometrical optics of any lens or mirror, the line through the source parallel to the axis of the optics does not necessarily represent an actual ray, but rather is included as a way of easily identifying where the image is located. It is used because the optics is assumed to have the property that all rays from the source to any part of the lens (or mirror) are bent in such a way as to converge on some other point (the image) and the mathematical form of the rule describing how this bending occurs makes sense for all points in the plane of the lens (or mirror) regardless of whether or not they are actually on the lens or mirror (and so regardless of whether or not the deflection actually occurs).

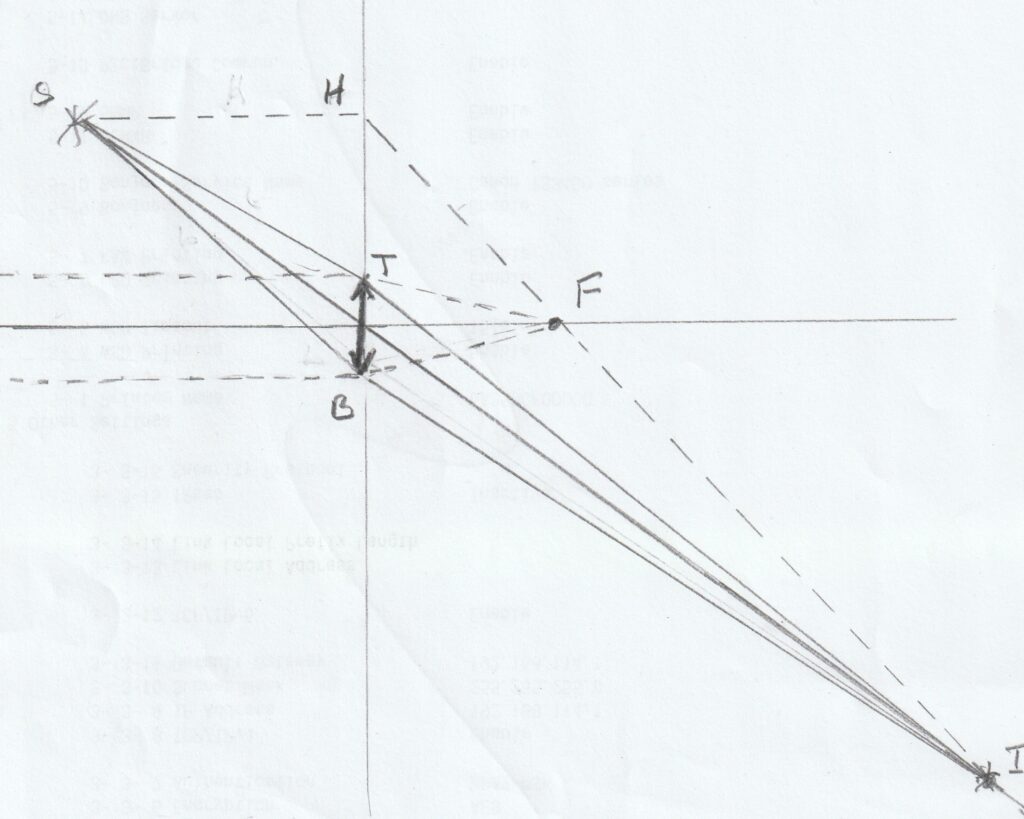
It is actually possible to calculate the angle of deflection for each ray (either by an algebraic formula or a geometric construction), and so to just use rays which pass through the lens (such as those through T and B, which I have shown as solid lines in the picture) without any reference to the imaginary ray (shown as a dashed line in the picture) which would bend at H if the lens was big enough; but the formula or construction is simplest for that imaginary ray and it works just as well as any other for determining the image point.

Source: (1003) Alan Cooper’s answer to How do you draw the image of the light source through the converging lens if the light sources are located higher than the top of the lens (it is not allowed to extend the lens)? – Quora

Block Universe Nonsense

A Quora question asks: Is it true that the past still exists and the future is predetermined? Is the ‘’block universe’’ correct, since Special relativity is scientifically proven? – Quora

No. It’s not true that in the context of Special Relativity “the past still exists”.

In fact, according to Special Relativity (which does appear to be correct for situations where the effects of gravity are negligible – though nothing outside of mathematics is ever “scientifically proven”), the whole idea of the (unique) past is meaningless since there are events that you consider past that are not in the past for a remote relatively moving observer who is at an event which you consider simultaneous with your present.

Also, again according to Special (and maybe* General) Relativity, the word “still” is also meaningless as its use at any time refers to events that are simultaneous with the statement, but that criterion will correspond to different sets of events for different observers.

*- I have added the word “maybe” since Viktor Toth# has mentioned that in General (but not Special) Relativity it is possible to identify a preferred set of inertial frames (in which the redshift due to expansion is the same in all directions), and these do share a common concept of simultaneity.

But of course, even in a Galilean universe, there is also the question of what you mean by saying that the past “exists”. Yes it exists as the past (and even in SR the past of my worldline exists as my past) but that does not mean it is happening now. And the same applies to the future. Even in a non-deterministic universe the future “exists”, as what will turn out to have happened, regardless of the fact that we have no way of predicting it.

#PS I am not linking to Viktor Toth’s answer because, despite having some good bits, I feel that it is marred by the inclusion of some very misleading (and quite unnecessary) statements about Quantum Mechanics.

Source: (1003) Alan Cooper’s answer to Is it true that the past still exists and the future is predetermined? Is the ‘’block universe’’ correct, since Special relativity is scientifically proven? – Quora

Another Quora Question

A Quora question asks: “How does quantum physics know that if a system were not measured it would be in multiple possible states (without measuring it), and that when measuring it collapses into one definite state?”

Quantum theory doesn’t “know” anything. All it does is describe what we know and makes predictions about what we may find out in future. What we call the “state” of a system is just a summary of what we know about it, and a system on which we can gain no new information without losing some of what we already have is said to be in a “pure” state.

An example is the case of a single electron whose position we are ignoring (so it can be considered fixed) and whose only measurable property is the direction of its spin. If we first measure the spin component in the vertical direction (say that of the z-axis), then we will always find that the spin is pointing straight up or straight down; and if we repeat that measurement we will see that the direction is unchanged. But if we then follow that with a measurement in any perpendicular direction then we have a 50% chance of finding that the spin is now pointing in that new direction and 50% chance of its opposite. And if we now return to the original direction we find equal chances for pointing up or down.

Here, the spin up state is a pure state because we cannot determine the sideways component without losing information about the vertical component, but being in the up state is not the same as being in both left and right states at the same time, and it is also not the same as being in a statistical mixture (ie in one or other of those two states but we just don’t know which).

P.S. In either quantum or classical physics, a system that is not measured or which we have only measured incompletely may be in any one of several pure states with different probabilities, and we call the resulting state a statistical mixture; but that is not the same as being in multiple pure states at once.

Source: (1002) Alan Cooper’s answer to How does quantum physics know that if a system were not measured it would be in multiple possible states (without measuring it), and that when measuring it collapses into one definite state? – Quora

Bergson vs Einstein

After reading this article twice, and yet again the paragraph where the author purports to show that “it’s wrong to think that Bergson’s idea of duration can be assimilated into the idea of psychological time”,

I am still unable to find any explanation of the difference between our internally experienced psychological time (which, by the way can not necessarily always be “aligned with external clock time”) and “the first-person experience of (Bergson’s unmeasurable) duration” (which they appear to identify as the “lived time” in terms of which “An hour in the dentist’s chair is very different from an hour over a glass of wine with friends”).

On the other hand Steven Savitt’s “solution” does not address the subjective nature of duration and appears to just identify it with the non-subjective proper time associated with a possible observer’s world line – which seems to be just giving up on the idea of any special “philosophical” time as this has always been the only kind of time that is ever discussed in relativistic physics.

Source: Who really won when Bergson and Einstein debated time? | Aeon Essays

Is Heat Radiation Just Infrared? 

It’s really no different than with any other kind of energy. Heat is basically just energy that is disorganized ie distributed in a way that is too complicated for us to keep track of – like the random motion of molecules in a gas as opposed to bulk motion or pressure waves in that same gas.

With regard to electromagnetic radiation, every hot body emits a broad spectrum of disorganized electromagnetic radiation at all frequencies – not just infrared (though that is the dominant range at the temperatures we normally experience); but it is also possible to produce organized electromagnetic radiation (eg from electronic circuits and lasers) and this is not “heat” even when it is infrared (though it can be used to create heat when absorbed by a body – just as organized mechanical energy can be converted to heat by friction).

Source: (1002) Alan Cooper’s answer to Is all electromagnetic radiation considered heat? Or just infrared radiation? – Quora