All I know for sure is that any cat whose owner would subject it to such an experiment cannot have been “Wanted”.
But if Schrodinger had had many cats to try this on I guess about half of them would be dead and the other half alive. And in all cases the “collapse” would have occurred long before the box was opened – or rather never, because a cat could never be put into a pure quantum state in the first place.
The “state” of a system that is studied in quantum mechanics is not a property just of the system itself but rather is just a summary of what is “known” about it by a class of outside “observers” which do not interact with it in any way between “observations”. (The “observers” don’t actually have to be conscious; anything such as a measurement apparatus that could be changed in some macroscopic way by interaction with the system could play the same role, with the relevant change being identified as “knowledge” so long as different macroscopic states of the “observer” end up associated with different values of whatever property is being “observed”.)
This relative state changes whenever the observer learns something about the system – and since since this results in the probabilities of all values other than the one observed becoming zero (while the one experienced by the observer becomes certain from the observer’s point of view) it is sometimes called “collapse” – though it should be noted that the total of all the probabilities remains the same, so it might be better to think of the probability distribution being collapsed “sideways” onto the observed value rather than “down” to zero everywhere.
As an example, consider the case of an electron that has just passed through a selector that ensures that its spin in the z-direction is positive (let’s call this “up”). If we think of the spin of the electron as a system in its own right and if we can control the path of the electron without interacting with its spin, then we can represent (what we know about) the spin by a quantum state, and it turns out that if we know the spin is up then we cannot assign any particular value (say left or right) to any horizontal component. All we can say is that if we pass many such electrons through another vertical spin selector they will all measure spin up, but if we measure in any horizontal direction we’ll get positive and negative results with probability 1/2 each. BUT (and here’s the “collapse”) if, on doing that horizontal measurement, we observe spin (say) left, then when we subsequently measure the same horizontal spin we’ll get the same result with certainty and the probability of seeing right will have gone down to zero (while if we go back to measuring the vertical component it will now have equal chances of being up or down – which is another reason for not liking the “collapse” language since what collapses one distribution has spread out another, and in particular has raised the chance of seeing down next time from 0 to 1/2).
Note: Jonathan Joss makes a similar objection to the word “collapse” and suggests that it be called a “rotation” of the state vector (but of course in the relevant Hilbert space rather than physical space).
Yes, it is true that “either twin could be considered to be moving at close to the speed of light”. And it is also true that so long as neither of them accelerates each will think that the other is ageing more slowly. But this is no paradox as there is no way for them to get together to see who is right. That can only happen if one or other of them turns around. And in that case whoever turns back towards the other will end up thinking that the other aged so much more quickly during the turn-around that when they get back together there will be a well-defined answer to the question of who is indeed younger and by how much. (They will not agree on the exact pattern of “when” the different ageing rates occurred, but since there is no absolute definition of “when” for events that do not happen at the same place, that disagreement is just a matter of having different points of view.)
Time does not even exist without some frame of reference, as space and time are just ways of assigning coordinates to events and different observers may do so in different ways. And in terms of any particular frame of reference, motion through space is usually thought of as having different positions at different points in time. Since the position varies with the time I suppose this could be described by saying that we “move with time”. But the idea of motion through time is kind of vacuous since any choice of time coordinate obviously changes when it changes; so I guess we could always be described as moving with time through the same time at “speed” one. This might get more interesting for the case of different reference frames with different time coordinates – in which case one might be moving with the time of one frame through the time of another (with a rate that would correspond to the Lorentz time dilation factor corresponding to the relative speed between the two frames).
So whether you are moving through space or time depends on what coordinate system you are using. In terms of coordinates based on your own body you are always fixed in space and “move” only through time. But in terms of the coordinates of a frame that is moving with respect to you, you are moving through its version of space (with exactly the opposite velocity).
That depends on what you mean by “horizontally oriented”. But if we take it as meaning perpendicular to the radius and parallel to the surface of the Earth (or any other sphere), then no matter which “horizontal” direction you look, you will not be looking directly at the horizon and the angle of depression down to the horizon will be the same in all such directions. So the horizon should appear perfectly straight in any undistorted(*) view of that sort. It will appear curved up at the edges if your line of sight is pointing upwards and down at the edges only if you are looking downwards (which is why all those pictures taken from airplanes claiming to refute “flat earthers” are so silly).
What does show the curvature of the Earth (albeit in a way that is very hard to notice even at the highest commercial airplane altitudes) is the fact that, when you look out “horizontally”, the horizon is below the midpoint of the picture (which is almost impossible to demonstrate convincingly with a photograph since there is no way of proving that the picture has not been cropped from one where the horizon was above the middle).
Of course, if you are far enough from the sphere that the only way any part of it can be in your field of view is by looking downwards (as in the various pictures of the whole Earth taken from space), then you will indeed always see the curvature if you can see any part of it at all. But at any altitude achievable by a commercial aircraft you will almost surely not.
In particular, even at an altitude of 64 km (which is well above most commercial airline cruising heights) we have the following:
An altitude of 64km is just a bit less than 1% of the radius of the Earth, so the angle of depression of the horizon is about arccos(0.99) (* – see first note below if you need an explanation), which is approximately 8 degrees. Since that is about 10% of the 80 degree viewing angle of a 24mm wide angle camera lens, a “horizontally” oriented camera with a wide angle lens at an altitude of 64 km should produce an image of a perfectly straight horizon line about 10% below the middle of the frame. (With a fisheye lens the viewing angle is 180 degrees so with such a lens the horizon should still be a straight line but just [math]8/180\approx 4.4[/math]% below the middle.)
If the camera is pointed down so that the middle of the horizon is at the centre of the frame then with the fisheye lens (if you could put it outside the window, or perhaps be working in the cockpit with a wrap-around canopy window) the horizon should appear as a half ellipse with the edges still about 4.4% down from the middle.
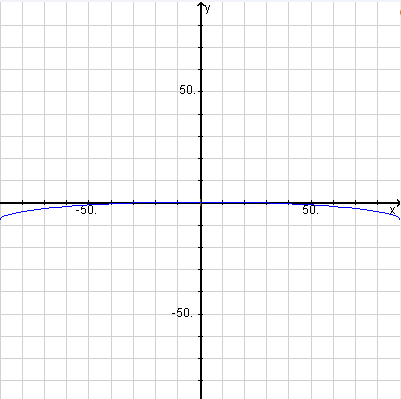
But for a normal wide angle lens, since the half-view width of 40 degrees [per https://expertphotography.com/wide-angle-lens/ ] is less than a half of the 90 degree sweep to the side of the camera, and since the equation of the ellipse is quadratic rather than linear, the edges of the part of the horizon in the picture from that lens will be less than [math]\frac{4\text{%}}{2^2}=1\text{%}[/math] of the image height below the middle.
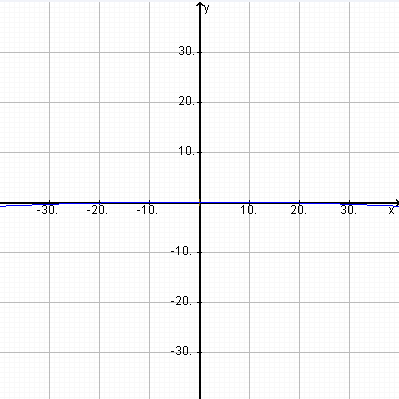
And with a telephoto lens of viewing angle just 10–20 degrees, the horizon should only be completely straight if it is right near the bottom of the picture, but the curvature that comes from pointing the camera down to centre the middle of the horizon should be even less noticeable as the image only shows 5 to 10 degrees worth of the drop. (** – See the second note below for the actual calculations)
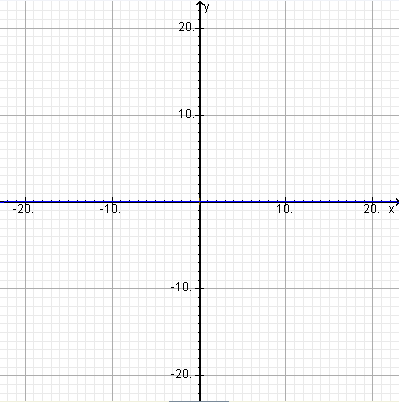
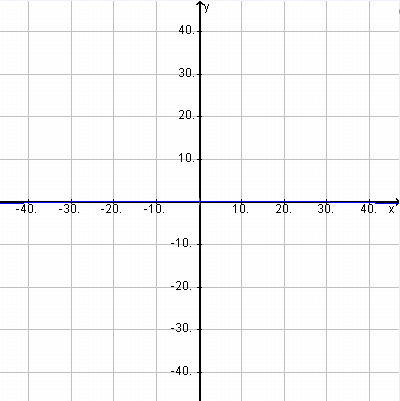
But at the typical 10km cruising altitude of a commercial airliner there is really no visible effect. The angle of depression of the horizon at that altitude is arccos(0.998) which is less than 4degrees, so in a square picture shot with a normal 50mm focal length showing just the middle 46 degrees of the 180 degree full sweep the drop from centre to edge of the horizon should be less than 0.0015 of the height of the picture (ie just barely one pixel down at the edges in a 640×640 image) – as shown below.
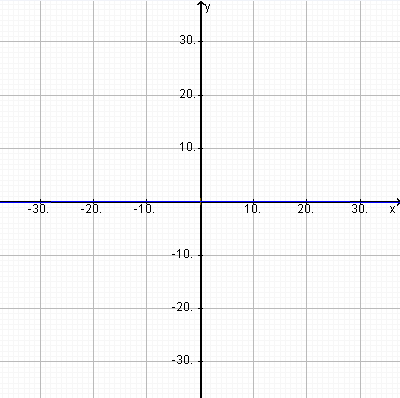
With a 28mm wide angle lens, showing the middle 75 degrees the amount only goes up to about .004 of the image height or less than 2.5 pixels in 640.
With the 94 degree sweep of a 20mm extreme wide angle we still only get a downturn of .0065 of the image height or about 4 pixels in that 640×640 image.
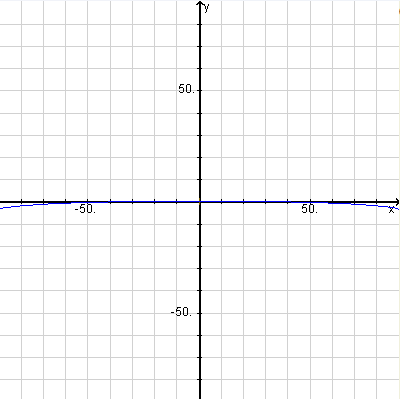
And even with the full 180 degree sweep of the unobstructed fisheye (whose picture compresses what would be in our peripheral vision down into the middle of our field of view and so gives a much more dramatic effect than what we actually see even from that panoramically windowed cockpit) the drop to the edges of the horizon line is only 2% of the image height.
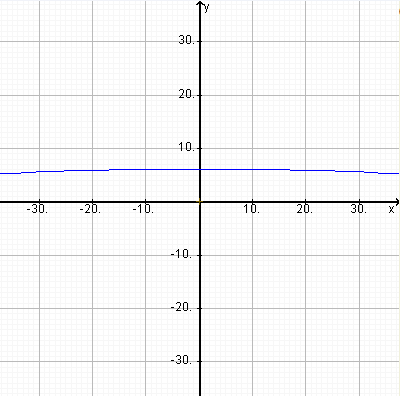
So, while it may be possible for a pilot in a cockpit with good visibility out of front and side windows to get a sense of curvature from peripheral vision, no picture taken from a passenger seat can show curvature unless the camera is pointed downwards (which is a natural thing to do from a plane since most of the interesting stuff is below the horizon).
Here’s what a picture from an ordinary wide angle lens should look like if the camera was pointing ten degrees downwards:
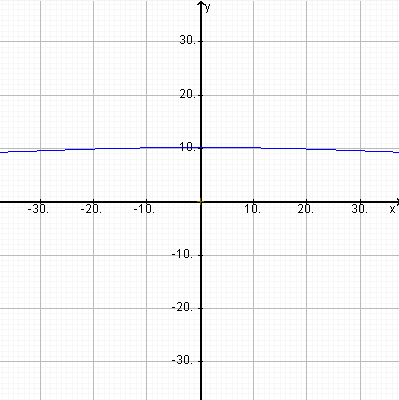
But if you are inclined to see this as evidence of curvature then compare it with the following view of what the same camera would produce looking 10 degrees downwards on a perfectly flat Earth:
(*)-Note1: The picture below shows that the angle of depression, [math]\delta[/math], is the same as the angle subtended at the Earth’s centre between the observer and the point seen on the horizon, whose cosine is just the ratio [math]\frac{R}{R+a}[/math] where [math]R[/math] is the radius and [math]a[/math] is the altitude of the observer.
(**)- Note2: If the edge of a circle is at an angle of [math]\delta[/math] degrees below eye level in all directions, then tilting the view down to bring the part directly in front up to the middle of the picture will not change the fact that the parts off at 90 degrees in the left and right directions are still depressed by an angle of [math]\delta[/math] degrees (and if we had eyes in the back of our head they would be looking up so that the part of the circle behind us would be further down at an angle of [math]2\delta[/math] degrees). Since the projection of a circle is an ellipse, the image of the half-circle in front of us would be given analytically (in terms of the image coordinates [math]x[/math] and [math]y[/math] being the numbers of degrees to the right and above the centre of the image) by the part of [math](\frac{x}{90})^2+(\frac{y+\delta}{\delta})^2=1[/math] with [math]y>-\delta[/math] (or parametrically by [math]x(t)=90cos(t), y=\delta sin(t)[/math] for [math]0<t<\pi[/math]). A fisheye lens would produce an image in which the [math]x[/math] and [math]y[/math] values range from -90 to +90, but with a lens of view width [math]w[/math] degrees the ranges in the picture would just be from [math]-w/2[/math] to [math]w/2[/math], and the images shown above were created by just zooming in on a graph of the ellipse so that the relevant ranges of [math]x[/math] and [math]y[/math] fit into the area of the picture.
640*4(1-sqrt(1-(94/180)^2))/90
90cos(t);4sin(t)-4;0,3.14
Source: Alan Cooper’s answer to Why isn’t there any curvature at the horizon when we look out if we live on a ball? – Quora
Note: For photographs illustrating how the angle of view affects apparent curvature (including its reversal for an upward pointing camera) see Figures 3 and 4 in this article. But be aware of the fact that the “barrel distortion” which that paper attributes to the design of the optical system is actually nothing more than the effect of an undistorted linear projection.
(*)There is more to this than just lens distortion as is also involves the projection of our (hemi)spherical field of view onto the flat plane of a picture (and no such projection can correctly reproduce the visual experience from all distances). If the projection displays equal angles from the optical axis as equal distances from the centre of the picture then the image of a circle drawn on a flat plane below the viewer appears as a straight line in an undistorted picture taken from directly above its centre with direction of view parallel to the plane. Pointing the camera down raises the middle features of the image and so makes it appear to curve down at the edges and pointing it up lowers the middle so that the edges appear to curve up. There is no curvature at all in such an undistorted truly horizontal projective view of the horizon from any altitude, and no noticeable curvature in an undistorted narrow angle view from 35000ft unless that view’s optical axis is well below the horizon.