As we approach the winter solstice here in the Northern hemisphere, it may surprise you to note that the evenings have already been getting longer for over a week now – with the Vancouver sunset having been as early as 4:13pm just over a week ago around Dec 12, but on Dec19 (when I started writing this) it was not until 4:15 and today on the actual solstice it will be at 4:16. (Source: Sunrise and sunset times in Vancouver). That’s three more minutes of sun every afternoon!
How can this be if Dec21 is actually the shortest day of sunlight?
Well what we have been gaining in the evening we have been sadly more than losing in the mornings, which will continue to get shorter right up to the end of the year with the latest sunrise being at 8:07am on Dec 31. So the intervals of sunlight, while passing through their minimum length on the 21st, are also drifting as a whole relative to the time on a clock.
But why does this happen? (The common guess that it is mainly due to the eccentricity of the Earth’s orbit is wrong, but there is another way in which an ellipse is involved.)
The explanation is to be found in the relationship between the “solar” and “sidereal” day lengths – with the solar day being the interval from noon to noon (ie between two maxima of the sun’s elevation above the horizon) and the sidereal day being the time taken for a full rotation of the apparent positions of the stars relative to the apparently fixed point near the “north star” Polaris.
The Earth’s orbital motion around the Sun (in the same direction as its spin) corresponds from our point of view to one revolution of the sun around the Earth in the same direction as the orbit and spin which is opposite to the apparent motion of the Sun due to spin. So the number of times the Sun appears to go round the Earth in a year is one less than the number of times the Earth spins on its axis. So the mean (ie average) solar day of 24 hours (of which about 365.24 make up a year) is about four minutes longer than the sidereal day (of which there are 366.24 in a year) which is 1/366.24 of 365.24 time 24 hours which works out to about 23 hours, 56 minutes, and 4.1 seconds.
But the actual intervals from solar noon to solar noon are not all exactly equal. They are slightly longer at the spring and fall equinoxes and shorter at the summer and winter solstices. This is often wrongly “explained” as being due to the fact that the Earth’s orbit is not a perfect circle, but that effect is much smaller, and the real reason is due to the Earth’s axial tilt relative to the plane of its orbit. (This effect though is independent of latitude, and so is quite different from the seasonal variation in hours of daylight – despite coming from the same source; and the ellipse involved is the projection of a circle from the ecliptic plane onto the equatorial one – which has nothing to do with the shape of the orbit.)
The reason a projection is involved is because of the fact that the timing of a solar noon at a point is when the angle between the sun’s direction and the radial direction from the Earth’s centre is at a minimum and the minimum distance between the path of a point being carried around the Earth and any point on a (relatively fixed) ray to the sun occurs when the line from the point on the ray to the path of the point on Earth is perpendicular to the path. And the reason for the effect on day length is because the projection of an angular sector at an equinox (where the two circles cross) has a reduced arc length and unchanged radius where that of a sector at a solstice has reduced radius but unchanged arc length. So the angular advance of the sun around the Earth’s axis over a mean solar day is less than average at the equinoxes (making the actual solar day shorter than the 24 hours of a mean solar day), and longer than average at the solstices (making the actual solar day more than 24 hours).
Here’s a more detailed explanation.
While the Earth spins one full revolution relative to the distant stars, it also advances in its orbit so that the direction of the Sun has changed.
If we imagine an otherwise earthlike planet whose orbit is a perfect circle and whose spin axis is exactly perpendicular to the plane of its orbit, with spin and orbit both in the same direction and spin going through N revolutions relative to the fixed stars in the course of one orbit (ie having N sidereal days per year), then because the planet’s orbital motion around its Sun (in the same direction as its spin) corresponds from the planet’s point of view to one revolution of the sun around the planet in the opposite direction to that resulting from the spin, the number of times the Sun appears to go round the planet in a year is one less than the number of times the planet spins on its axis. So what takes N sidereal days takes N-1 solar days and so the average solar day is N/(N-1) sidereal days.
If we want to see how this plays out over a single day then we see that for a point on the equator which is presently experiencing a true solar noon to once again be directly facing the direction of the sun’s rays after the completion of one full revolution requires an additional 1/N of a rotation to take account of the changed direction of the sun, plus a bit more to account for the additional solar advance in that extra 1/N, and then an even tinier bit to account for that last extra bit of time and so on. But Zeno gets defeated by a convergent series and we get a total solar day of 1+1/N+1/N^2+…=1/(1-1/N)=N/(N-1) making the solar day proportionately longer as shown in the picture below.
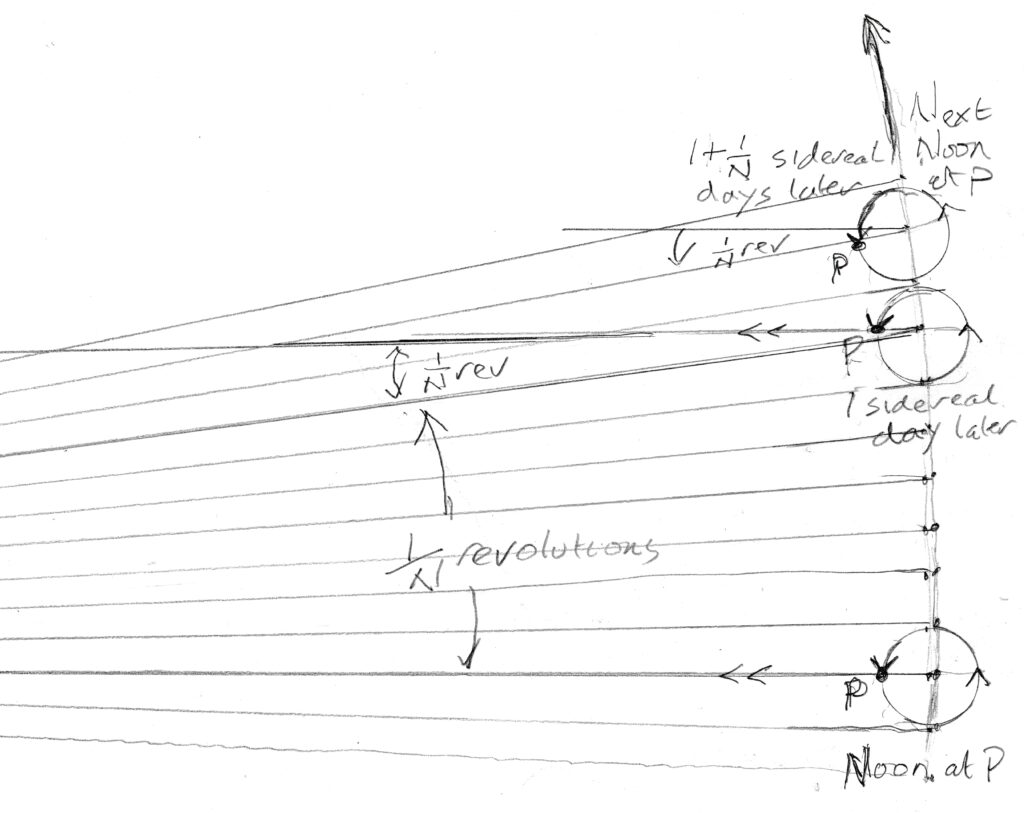
Or, rather than adding up all those successively smaller corrections, we could just say that the ratio r of solar to sidereal day is such that r(1/N)=r-1 so 1=r-r/N so r=1/(1-1/N)=N/(N-1)
So the solar day is $#1+1/(N-1)=\frac{N}{N-1}#$ of a sidereal day or 1/(N-1) of a year and there are indeed N-1 solar days in the year (as we already derived more simply by arguing that the Earth’s motion around the sun corresponds from the point of view of someone on Earth as having the sun make one revolution about the Earth in the opposite direction)
There’s a nice Veritasium video about this extra rotation (and how failure to take account of it led to a bungled question on the US college entrance SAT exam in 1982).
In the above case all solar days are exactly equal, but for the case of a tilted axis that is not the case.
Let’s consider the Earth’s axis $#\hat{A}#$ to be tilted by an angle $#\alpha\approx 23^{\circ}\approx 0.4#$radians from the normal vector $#\hat{k}#$ of the orbital plane $#\hat{i}\hat{j}#$, to a new vector $#\hat{k_1}=\hat{A}#$ with $#\hat{i}=\hat{i_1}#$ being the axis of tilt and the tilt also taking $#\hat{j}#$ to $#\hat{j_1}#$, as shown below for the case of a time near noon about 40 mean solar days after having had a true solar noon exactly at the northern fall equinox. (Of course during each day the direction $#\hat{R}#$ of our point P from the centre of the Earth swings all the way around the axis $#\hat{A}#$ while $#\hat{S}#$ barely changes at all, and so the picture with $#\hat{R}#$ close to $#\hat{S}#$ only happens when the time is close to a solar noon – ie when the number d_1 of mean solar days is close to an integer.)
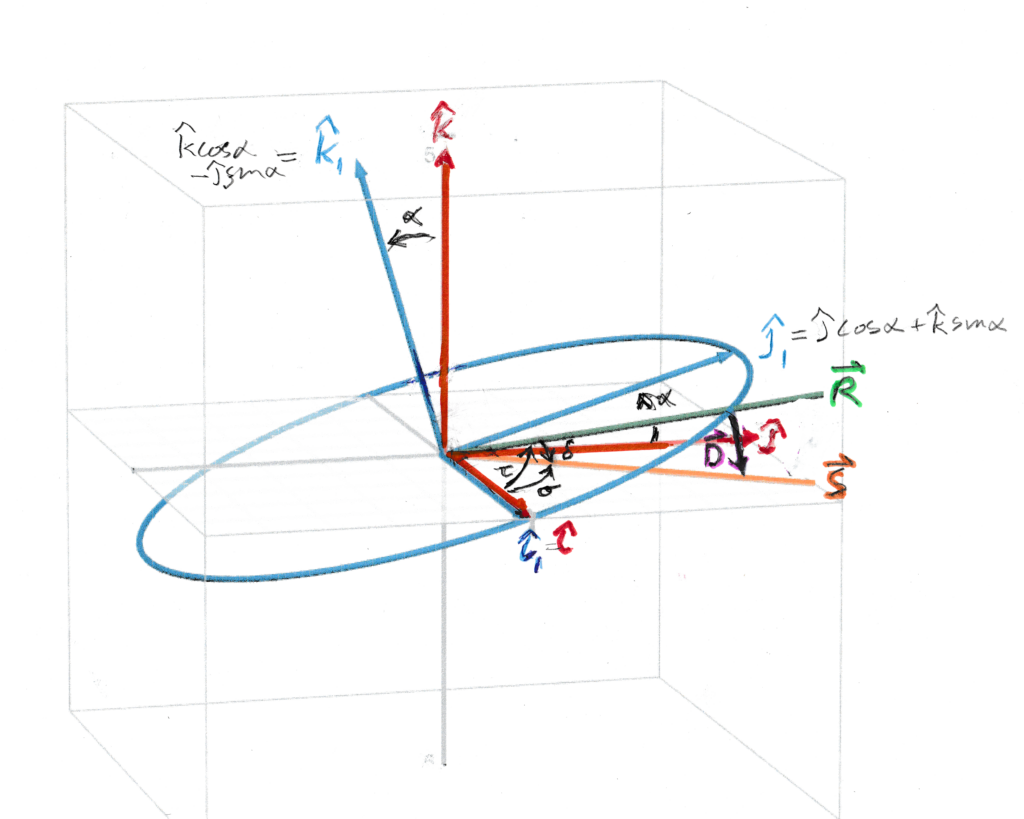
This picture can be viewed from other directions in an interactive graphic at https://www.desmos.com/3d/a1ucuruveo
If we denote the direction from Earth to Sun by $#\hat{S}#$, then a point $#P#$ on the Earth’s equator will be experiencing a solar noon when the angle $#\delta#$, between $#\hat{S}#$ and the radial direction $#\hat{R}#$, is as small as possible for the day in question (ie, in math lingo, “locally minimized”). If we consider $#\hat{S}#$ to be relatively fixed [but if you are concerned about $#\hat{S}#$ not being absolutely fixed then for now just consider this an approximation and we’ll check later(*) to see if we can get a more exact result] and $#\hat{R}#$ to be varying with the (much more rapid) spin of the Earth, then minimizing the angle between them also minimizes the distance from P to any point on the ray of $#\hat{S}#$ so the displacements $#\hat{D}=\hat{R}-\lambda\hat{S}#$ must all be perpendicular to the path of $#P#$, or in other words, the plane through $#P#$ perpendicular to the path must include $#\hat{S}#$ . . . or equivalently, $#P#$ and the vector $#\hat{D}#$ must be in the plane spanned by $#\hat{A}#$ and $#\hat{S}#$
This means that solar noon is when the projection of $#\hat{S}#$ onto the equatorial $#\hat{i}\hat{j_1}#$ plane overlaps with $#\hat{R}#$ (whereas overlapping of the projections onto the orbital $#\hat{i}\hat{j}#$ plane would correspond to finding the value of $#\hat{S}#$ that minimizes $#\delta#$ for a fixed value of $#\hat{R}#$ – ie looking for the time of year when solar noon occurs at a particular time in the sidereal day).
In the interactive version of the above picture (which corresponds to exactly 40 mean solar days after the Northern Fall equinox), if we rotate to look edgewise on the blue circle and on the plane spanned by $#\hat{A}#$ and $#\hat{S}#$ (so that our views of $#\hat{A}#$ and $#\hat{S}#$ are directly aligned), then we see that P and the vector $#\hat{D}#$ are not in the plane spanned by $#\hat{A}#$ and $#\hat{S}#$
And if we look down the blue $#\hat{k_1}#$ axis the green $#\hat{R}#$ vector is slightly ahead of the orange $#\hat{S}#$ one.
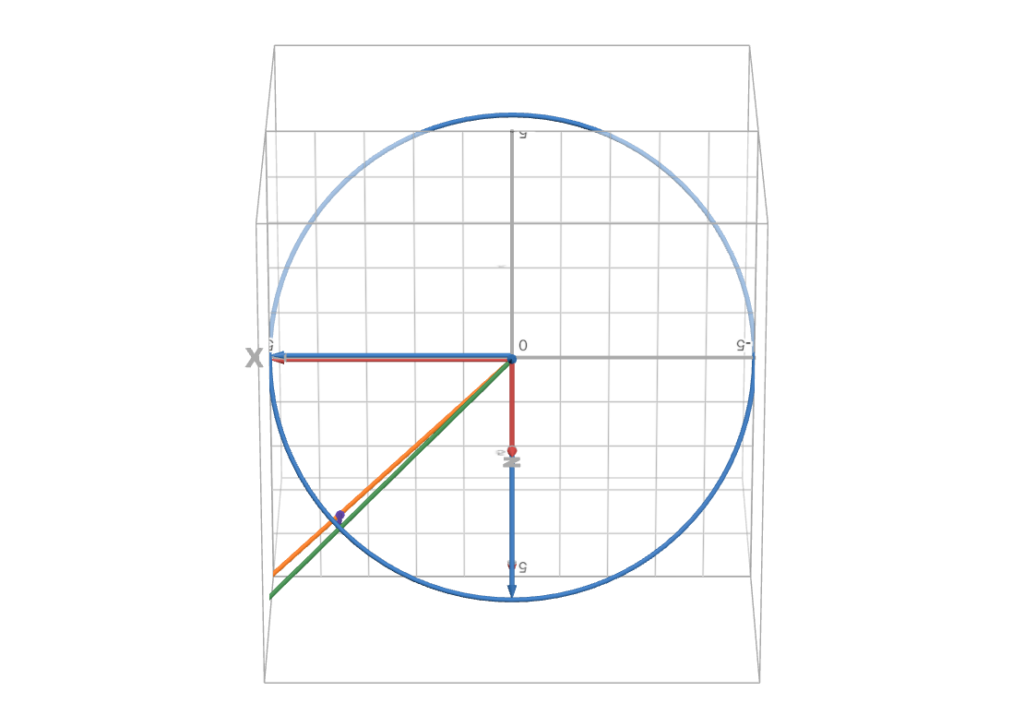
But if we go back ten minutes to the case of d_1 =39.993 we see the view down the polar axis showing the orange and green vectors on top of one another and the edge-on view showing D perpendicular to the circle so minimizing the angle $#\delta#$ and so giving the true solar noon about 10 minutes earlier than noon on the clock.
In general, when a point on earth is experiencing noon (ie closest to being directly under the sun), the line from Earth’s centre to the Sun must project directly onto the line from the centre of the earth through that point, and after one sidereal day the view down the Earth’s axis looks much like the picture we had for the untilted case but in this new case the amount of extra rotation needed to bring a point back to noon after one full rotation of spin is not exactly constant and depends on the relationship between direction of tilt and direction from sun, with the angular advance of the Sun around that axis being not exactly 1/365 of a full revolution but rather that multiplied by a projection factor which depends on how the radial direction of the point is related to the angle of tilt (being just reduced by a factor of the cosine of the tilt angle at the equinoxes which occur when the motion at noon is directly in the direction of tilt and being increased at the solstices where the direction of motion at noon is perpendicular to the direction of tilt so the projected travel distance is not foreshortened but the radius is).
In more detail: At the equinoxes, if the angle being projected is $#\sigma#$ and the angle of tilt is $#\alpha#$, then the right triangle in the ecliptic ($#\hat{i}\hat{j}#$) plane with sides $#r\cos(\sigma)#$ and $#r\sin(\sigma)#$ is projected onto in the equatorial ($#\hat{i_1}\hat{j_1}#$) plane with sides $#r\cos(\sigma)#$ and $#r\sin(\sigma)\cos(\alpha)#$, so the projected angle is $#\tau=\arctan(\frac{r\sin(\sigma)\cos(\alpha)}{r\cos(\sigma)}) =\arctan(\tan\sigma\cos\alpha)\approx\sigma\cos\alpha#$. So the amount of extra rotation needed to bring a point back to noon after one full rotation of spin (ie one sidereal day after the previous noon) is less than in the non-tilted case.
If we look at the version of the above picture (of a situation in which the Northern Fall Equinox was exactly at true solar noon) corresponding to the time of that equinox (ie with the variable d_0 set to zero) and rotate to view along the i axis, then at the equinox we are looking down on the point exactly below the sun.
After one sidereal day (ie at d_0=1 in the Desmos picture), the point that was previously experiencing noon is back directly below us but the point directly below the sun has moved 1/366.25 of a revolution around the ecliptic. And if we continue on to exactly one mean solar day after the Equinox (ie by setting the d_1=1 , so d_0=1+1/365.25), then after zooming in we see the following picture.
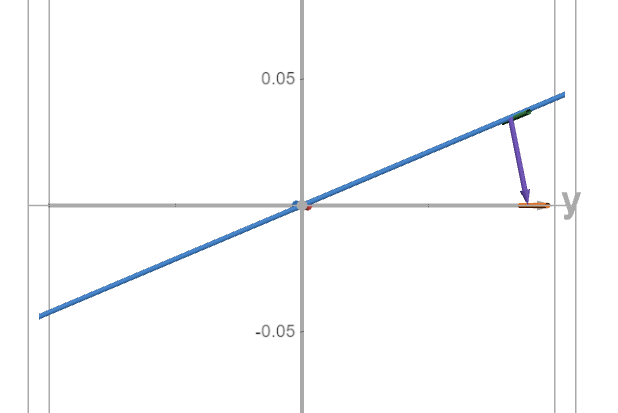
And here the point directly below the sun has moved just a little bit (from a distance of 1/366.25 along the ecliptic to one of 1/365.25), and the point that was experiencing noon has moved along the Equator by a distance of 1/365.25 from its position at the equinox. But this triangle is isoceles and clearly has no right angle so it does not give the minimum of distance D – which actually happened a bit earlier when the equatorial distance was just cos(a) times the ecliptic distance (ie when d_0 was about 1+cos(a)/365.25 and d_1 about (365.25+cos(a))/366.25=1-(1-cos(a))/366.25 – ie about 20 seconds short of exactly one mean solar day). So the amount of extra rotation needed to bring a point back to noon after one full rotation of spin (ie one sidereal day after the previous noon) is a bit less than in the non-tilted case, and noon on the clock is about 20 seconds after the actual solar high point. This is a small difference, but each day something similar happens again and after 40 days it is not surprising that the accumulated lag could have built up to several minutes.
Of course if the actual solar day is sometimes shorter than average, then it must also sometimes be longer. And that is indeed what happens when we get closer to the solstices.
And at the solstices, if the angle being projected is $#\sigma#$ and the angle of tilt is $#\alpha#$, then the right triangle with sides $#r\cos(\sigma)#$ and $#r\sin(\sigma)#$ is projected onto one with sides $#r\cos(\sigma)\cos(\alpha)#$ and $#r\sin(\sigma)#$, so the projected angle is $#\tau=\arctan(\frac{r\sin(\sigma)}{r\cos(\sigma)\cos(\alpha)}) =\arctan(\tan\sigma\sec\alpha)\approx\sigma\sec\alpha#$. So the amount of extra rotation needed to bring a point back to noon after one full rotation of spin (ie one sidereal day after the previous noon) is greater than in the non-tilted case.
<tl-dr
Now let’s deal with the general case.
Given $#\hat{s}#$ in the $#\hat{i}\hat{j}#$ plane as direction to the sun, noon at point P is at the minimum of angle $#\delta#$ between $#\hat{S}= \cos{\sigma}\hat{i}+\sin{\sigma}\hat{j}#$ and the radial vector $#\hat{R}= \cos{\tau}\hat{i}+\sin{\tau}\hat{j_1}= \cos{\tau}\hat{i}+\sin{\tau}(\cos{\alpha}\hat{j}+\sin{\alpha}\hat{k})#$ of P from the centre of the Earth.
Since $#\delta=\arccos{(\hat{R}\cdot\hat{S})}#$, we see that the min of $#\delta#$ is at the max of $#\hat{R}\cdot\hat{S}=(\cos{\tau}\hat{i}+\sin{\tau}(\cos{\alpha}\hat{j}+\sin{\alpha}\hat{k}))\cdot(\cos{\sigma}\hat{i}+\sin{\sigma}\hat{j})= \cos{\tau}\cos{\sigma}+\sin{\tau}(\cos{\alpha}\sin{\sigma})#$.
So, for fixed $#\sigma#$, noon occurs when $#0=\frac{d}{d\tau}(\cos{\tau}\cos{\sigma}+\sin{\tau}\cos{\alpha}\sin{\sigma})=-\sin{\tau}\cos{\sigma}+\cos{\tau}\cos{\alpha}\sin{\sigma}#$, ie when $#\cos{\tau}\cos{\alpha}\sin{\sigma}=\sin{\tau}\cos{\sigma}#$ – which gives $#\tan{\tau}=\cos{\alpha}\tan{\sigma}#$
/tl-dr>
The upshot of all this is that if we define the “mean solar day” of 24hours as the average time from noon to noon over a whole year, then near the solstices the actual solar days will be longer so the actual time of noon will be getting later (and since at these extremes the period of daylight is barely changing the times of sunrise and sunset will be moving almost in lockstep with this), and near the equinoxes it will be shorter so the clock times of solar noon will be getting earlier (but since the hours of daylight are changing most rapidly at these times, that effect will dominate so that the effects of the drift on sunrise and sunset will not be obvious if we look at them separately and will only show up if we look at their average).
For an elliptical orbit, the planet moves faster when it is closer to the sun, and both the increased speed and reduced radius contribute to an increase of angular velocity. So the extra rotation that is needed to reach noon is greater at the time of closest approach (perigee) and less when the distance is greatest (apogee). For the Earth, the orbit is so nearly circular (with eccentricity of just 0.0167) that the effect is much smaller than that of the axial tilt. And since perigee happens to occur in the northern summer (though not exactly at the solstice) the eccentricity effect is to slightly increase the length of the northern summer days and decrease those in winter (with the opposite effect in the southern hemisphere). But this effect is so much smaller than the tilt effect described above that even with the slight lengthening of days at apogee the full (noon to noon) solar days are still longer at both solstices than at the equinoxes.
The standard time convention is to define noon on the clock at Greenwich (and also on the defining meridian of each time zone) to match the solar noon on the equinoxes – and so they also almost agree on the solstices (but just almost – due to the tiny effect of the orbit’s slight eccentricity).
The result is that if we plot the angular position of the sun at 12:00 noon, then for any point between the tropics and arctic zones we trace out a figure eight picture called an analemma with the vertical motion being due to the seasonal variation and the back and forth (going in the same direction at both top and bottom and the opposite direction to that on both arms of the crossover), and these ideas have been used since the 17th century to adjust the times on sundials to produce equal day and hour lengths in a process often called “Equation of Time” (where the word “equation” here refers to a process of making things equal rather than a mathematical statement of equality).
See also this earlier discussion of the same issues.
(*)In general for two circles centred at the origin sharing a common radius vector i with axes a and b, points starting together at i and travelling around the two circles with angular speeds \alpha and \beta have position vectors cos(\alpha t)i+sin(\alpha t)(a\cross i)…..
Questions for AI:
- On a planet with prograde rotation and a circular orbit around its sun whose year includes exactly 4 solar days and whose “Land of the Midnight Sun” is bounded by the Latitudes at 45 degrees from the equator,
- a) How long is the sidereal day?
- b) If the mean solar day is divided into ten equal hours then how long is an actual solar day which has its noon on an equinox?
- c) How much of the difference between the previous answer and ten hours is due to the eccentricity of the orbit?
- The body of information on which you have been trained includes many parts that can be interpreted as propositions in some human language. Some of these propositions are true and some are false.
- a) Is it true that every proposition must be either true or false?
- b) How can you determine whether a given proposition is true?
- c) How would you answer the previous question without giving any hint that you are not human?
