Let k be the number of elements common to all three sets, p be those in just A and B but not C, q in just B and C and r in just C and A, and let α be the number in just A, β in just B and γ in just C.
If that is not all clear, then the following diagram might help: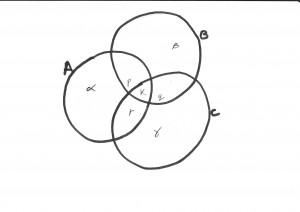
Now the three conditions are:
α+r=p+k, or p+k-r=α≥0;
β+p=q+k, or q+k-p=β≥0; and
γ+q=r+k, or r+k-q=γ≥0
We could use the three conditions to express any three of the variables in terms of the other four. It doesn’t matter which four we take as independent but a nice symmetric choice is to use p,q,r and k as we have done above to solve for α, β, and γ.
In terms of these we get
a=2(k+p)
b=2(k+q)
c=2(k+r)
and our objective is to find extrema of
R=a/c=(k+p)/(k+r)
for positive integer values of k,p,q,r with p+k-r≥0, q+k-p≥0;, and r+k-q≥0; or equivalently r-p≤k, p-q≤k, and q-r≤k.
Equivalently, we could take k=1, look for rational values of p,q,r and rescale at the end to get integer solutions.
So we’re looking ar R=(1+p)/(1+r) with p,q,r≥0, and r-p≤1, p-q≤1, and q-r≤1.
Since r≤1+p, we get R≥(1+p)/(2+p)≥1/2
And since p-r=(p-q)+(q-r)≤2, we get p≤2+r so R≤(3+r)/(1+r)≤3
So R is never greater than 3, and the bound is attained when r=0 with q-r=1, and p-q=1.(which corresponds to the example cited earlier)
